This past month I have been doing a book study with a few people in the blog world. So I am linking up with Sherrie at Middle School Math Rules as she is the one that started this book study! The book is called Minds on Mathematics - Using Math Workshop to Develop Deep understanding in Grades 4-8 by Wendy Ward Hoffer.
If this is your first time reading, please be sure to check out my notes from Chapters 1 & 2 , Chapters 3 & 4 , and Chapters 5 & 6. Also check out Sherrie's blog - Middle School Math Rules and see all the wonderful comments that have been left by many people doing this book study and the fantastic and thought provoking blog posts that have been written in regards to this book!
Now onto Chapters 7 & 8:
Chapter 7: Minilessons
Problem of the Day: How do you set students up for success as independent thinkers and problem solvers?
Postulate: We apprentice learners as mathematicians by explicitly teaching students how mathematicians use thinking strategies, make sense of and apply concepts to help them solve problems.
The one thing that stood out to me in this chapter is I need to step away from showing them "how" to do the math and start showing them how to "think" as a mathematician. I loved the line "typical instruction is all about giving a child a fish, while mini lessons are about teaching children how to fish." I really need to start thinking aloud in front of the students asking myself what do I already know and what do I need to find out? I also like the idea of discussing pitfalls. This will give you insight on a child's fears as they approach a complex problem. Last year a teacher at my school started doing something she called FAME (facts, art, math, explain). Each time the students came to a word problem, I had them use this approach. I realized then that it was a good strategy but it wasn't as good as I was hoping and that is because I did a poor job of modeling what I expected. This seemed to coincide with what Hoffer describes a teacher should be modeling during the mini lesson.
I liked the idea of at the end of the mini lesson asking "does anyone have any questions?" instead if "does everyone understand?" There is a big difference. Then letting the students answer!
I liked the chart on page 113, but it did seem very time consuming. I know we don't want to rush through the curriculum just to finish, but we are accountable for those pieces that we missed if we don't cover everything. Especially since there is a lot of pressure on testing, is it more important for your students to really understand just a few things or to have seen everything? It's going to be challenging to find the right balance.
I should have included this next diagram in the previous blog, but if this circle was the class period, here is how much time you would spend on a minilesson (the opening is the one just to the left of that):
So keep your minilesson short and sweet. This is also where I have questions about interactive notebooks-they look like they take a long time since they are so colorful/bright/interactive, so can you make interactive notebook work with the workshop model classroom? Does anyone have any success stories with interactive notebooks?
Chapter 8: Work Time
Question of the day: How can we facilitate thoughtful and productive work time for math learners?
Postulate: Students learn most when they spend math work time thinking, talking, and making meaning of mathematics for themselves.
 |
| The bulk of your time should be spent on Work Time |
This chapter gave me quite a few ideas: choosing groups, review games, project ideas & differentiation strategies. But it also left me with a few questions and most of them had to deal with time!
A dream work time would be self-direction, independence, and purpose as learners delve into rigorous content. But how do we get there?
Likes:
- On page 118 Hoffer described an old review game and then how she revamped it. I can really see the difference and I can also tell you that I am guilty of planning the same type of reviews as her first game. I love that when she revamped it, she had students staying behind and explaining to the other students how to do something.
- I really liked the grouping ideas on page 124 (appointment clock, card partners, and random). I need to do a better job of mixing up groups. And I also like her response to students who think they can't work with another student. "Yah, it can be really tough to collaborate. And it is one of the most important things you can learn in life. So, what are you going to do to work this out?" This is a problem solving skill and as mentioned before, problem solving goes way beyond math.
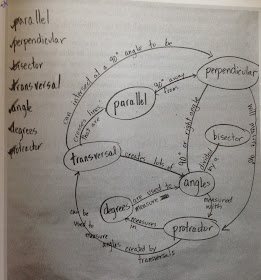
- I liked this mapping activity:
- I also need to do a better job of showing the students exactly what I expect as far as their work being neat and organized, putting units at the of the their answer, explaining the answer if it's a word problem... Good ideas are listed on page 127.
- Here is also a chart I liked of different ways to differentiate.
- I really liked her ideas for students getting stuck and how we need to answer a question with a question so our students do not rely on us to just give them the answer.
Questions I Still Have:
- I have always been told that choice is the key to motivation and I tried to keep that in mind last year, but sometimes it is difficult. I need to remember that "students do not need to do the exact same thing to show that they understand." -this struck a chord with me, as last year we worked on common essential skills. (We have 8 sixth grade math teachers at our school and we would all kind of stay together as far as where we were in the curriculum. After we finished a unit, each of us would give a common 4 question quiz (an example would be multiplying decimals) and then we would come together and share our data and discuss misconceptions and share the success we had). One of the main thing we discussed is that it is so odd that some students would fail these little essential skills quizzes, but yet, we knew they understood the content. It is still a mystery to me and I'm not sure how to move forward in our essential skills with questions like this. Does anyone else have essential skills at their school that are common among all the content teachers in your building? What are your thoughts on this?
- Under the Differentiation by Process (bottom of page 121), Hoffer mentions using several different tools/materials. I noticed last year that when I would present how to solve the problem in numerous ways, the students would get more confused and then they were concentrating on the how and not actually making sense of the problems. I worry that presenting so many options causes more confusion than anything; unless they had a lot of time to spend with each tool, but we just don't have the time to do that. However, a few times last year I would have 1 or 2 students who really weren't getting it, so I would get out some other type of manipulative and show them an alternative method. I did it on an as needed basis and not necessarily with the whole class. Has anyone else experienced this? What are your thoughts on having so many options?
- There is a project mentioned on page 122 and at first I thought it would be a good idea, but then I struggle with time. Is working on one project for 5 days, only looking at a couple problems worth that much time? What are you thoughts on this?
Please feel free to comment with any ideas, suggestions, comments, questions!








No comments:
Post a Comment